Towards LLM-based Experimental Economics

This blog post explores how Large Language Models (LLMs) can revolutionize experimental economics by simulating human behavior in foundational economic scenarios, while steering AI from zero-sum games to general non-cooperative games and agents towards strategic entities in a multi-agent environment. Traditional approaches in economics are limited by the costs and complexities of human-based experiments, and replacing humans with LLMs enables large-scale simulations, allowing researchers to examine a variety of economic mechanisms.

Introduction

There are three basic approaches to scientific studies: empirical, which relies on collecting observational data from real-world settings without intervention; experimental, which involves manipulating variables in a controlled environment to examine cause-effect relationships; and theoretical, which focuses on developing models and frameworks to explain or predict phenomena without direct data collection or experiments. In the context of economics, economic theory aims to make predictions using stylized models and solution concepts, mainly ones derived through equilibrium analysis. Experiments can be applied in the field or the lab, and the field of behavioral economics uses lab experiments to contrast theory prediction as well as to test alternative models, e.g. the introduction of prospect theory . Needless to say, empirical observations are the key to economic analysis; this analysis exploits e.g. econometric tools for evaluating economic predictions. Although different researchers have different biases towards these approaches, there is no doubt they all obtained significant success.

Game Theory and AI

Of particular interest is the field of game theory. This field has originated in close time and place proximity to AI. Indeed, some of the early Turing Award recipients in AI were roommates in the same graduate school as some of the early Nobel prize recipients in economics associated with game theory. Unlike former economic models, game theoretic models are very mechanistic and focus on detailed strategic aspects of well-specified interactions rather than focus on price equilibrium in large markets, making it ideal for synergy with work focusing on multi-agent systems in AI. Indeed, the field of RL, for example, is shared among these areas . Game playing has been central to AI for many years, and as early work in game theory, its focus is mostly on the so-called two-person zero-sum games. In these games, there are two players with fully complementary incentives. Such games can be shown to possess a value , and each player has an optimal strategy guaranteeing that value. In a sense, these games can be solved as linear programming and treated as an optimization problem.

Rock Paper Scissors is a classic zero-sum game where one player’s gain is another’s loss, keeping the total payoff constant. Here you can see the impact of the players' actions on the payoffs they receive at the end of the game. Player 1's payoff is marked in blue, and Player 2's payoff is marked in red. Each win, loss, or tie results in a net change of zero, illustrating the direct competition and balanced outcomes inherent in zero-sum dynamics.

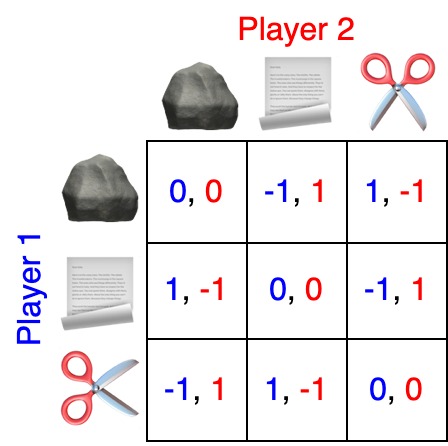
Modern work in economics, however, took very different directions from work in AI, mainly due to its focus on general non-cooperative games rather than zero-sum games. Indeed, when a seller tries to persuade a buyer to buy a product, there may be outcomes that are better for the seller and outcomes that are better for the buyer, but both have some joint incentive not to decline a mutually beneficial outcome.

A classic example of such a non-cooperative game is the persuasion game, involving two players: the sender and the receiver. The sender holds information about the state of the world that is only visible to them and can send a stylized message—a predefined, simple message—to the receiver. The receiver uses this message, along with their knowledge of the prior distribution for the state of the world, to make a decision. The combination of the actual state of the world and the receiver’s decision determines the payoff for both players. An instance of this game was presented by : in this game, the sender is a travel agent aiming to sell hotel nights regardless of the quality, while the receiver is a traveler who wants to stay only at high-quality hotels. Each round, a hotel is randomly selected. The travel agent knows the true quality of the hotel. On their turn, she choose whether to recommend the traveler stay at the hotel or to suggest staying home. The traveler uses the signal received from the agent to decide which action to take: go to the hotel or stay home. The sender’s payoff is determined by this decision: 1 if the receiver chooses to stay at the hotel, and 0 if they stay home. The receiver’s payoff is 1 if they stay at a good hotel or avoid a bad one, and 0 if they stay at a bad hotel or miss out on a good one. Note that when the hotel is good, the interests of both players align: both will benefit only if the receiver chooses to stay at the hotel. When the hotel is bad, their interests diverge.

In almost no case are economic games zero-sum games. This led to notions of equilibrium (fixpoint) solutions as predictions for behavior in economic interactions on the theory side. On the experimental side, such non-cooperative games have been tested, in some cases showing deviations from equilibrium outcomes, yielding quite a few powerful and celebrated behavioral theories based e.g. on learning , risk modeling , etc. The complex systems approach to economics also addresses such setups, particularly with many partially collaborative agents and the resulting non-equalibrium behavior (See for example). However, work in AI has mostly focused on optimizing agent behavior. When it comes to games, highly powerful techniques have been built for game playing a wide variety of zero-sum games, most recently leading to huge success using deep RL.

Illustration of the persuasion game where the sender (travel agent) recommends hotels to the receiver (traveler) based on private information about hotel quality. The traveler's decision depends on the sender's signal and their interactions from previous rounds. The payoff for both players is determined by this decision and the true quality of the hotel. (Illustration based on )

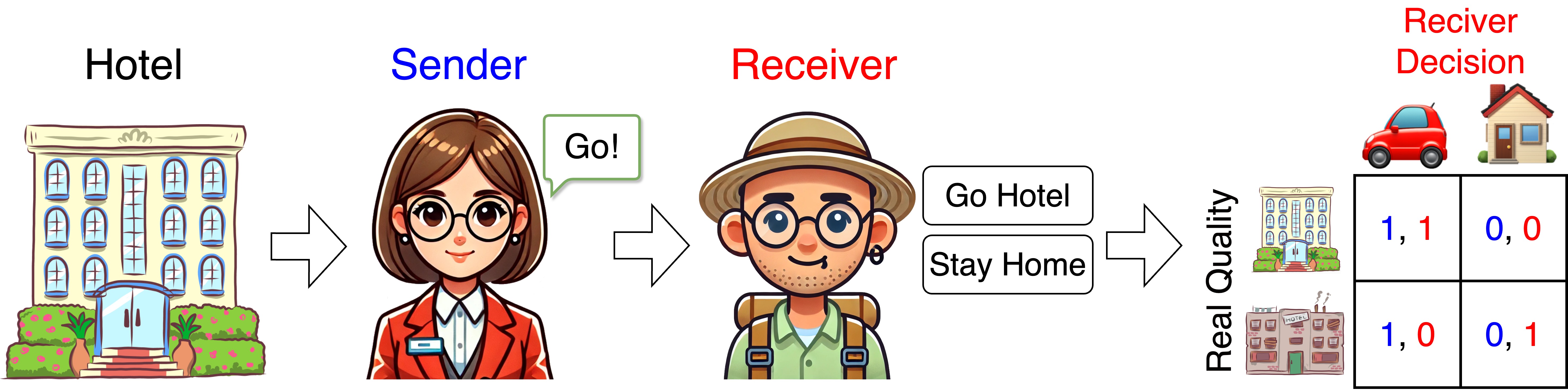
Challenges and Opportunities with ML and LLMs

As can be understood from the above, AI took an agent perspective dealing with computational agents in classes of games, highly connected to optimization, which are in most cases vastly different from fundamental non-cooperative games discussed in the economics literature. On the other hand, as the latter are not reduced to optimization problems the predicted behavior is non-trivial for analysis and/or for behavioral study. Indeed, both game theoretic analysis and its experimental study are highly limited, despite their shining successes; the game theoretic analysis is limited both by the fact analysis might become easily intractable and moreover by lack of “right solution”; the experimental study is limited due to very high cost and limitations of controlled experiments with human subjects. In recent years, computer scientists have looked closely at algorithmic aspects of game theory under the title Algorithmic Game Theory . While some of that work highly affected real-world systems (such as ad auctions), given the ML revolution, we are in the stage of bringing experimental economics to a whole new stage.

Both economic theory and behavioral economics lab experiments possess two desired properties: simplicity and controlability. In other words, they allow us to focus on studying well-defined tractable frameworks while isolating unobserved or hidden effects. Simplicity allows for easy analysis (e.g., computing an equilibrium, either as a solution or while refuting its fit), while controllability allows to overcome dealing with sophisticated causal effects of unseen variables. Indeed, the latter is one of the big challenges empirical studies need to address. The challenge, however, is that the above setups (a) might be too remote from real-world natural settings and (b) will not allow to experiment with a wide variety of settings when considering alternative economic mechanisms. These are exactly the aspects that the current ML revolution allows to handle.

To explain (a) above, consider the following. Celebrated sender-receiver / information design models in economics (persuasion, negotiation, bargaining) simply ignore the use of natural language while considering only stylized messaging! We believe a good compromise is introducing a desired property, which we term adequacy, and can be addressed by emergent ML technology. The adequacy requirement refers not only to incorporating natural acts such as natural language but also makes it possible to consider more elaborated versions of simplified settings such as ones taking into account repeated interactions. This may make the situation infeasible to analyze if we would like to achieve a “closed form formulas” predictions of behavior. One important example is the use of natural language, which has no natural fit with standard mathematical economic theory models. However, ML can come to the rescue. In this context, behavior in language-based non-cooperative games (where natural language is used) will be treated as an ML problem – given the training data of some users predict behavior of other users , or, as another example, given the agent’s behavior against some fixed partners, predict the behavior of other new partners (as in off-policy evaluation) . We refer to the ability to make useful predictions given such (more) adequate models as predictability.

In a language-based persuasion game, the sender sends a textual signal instead of a stylized message. The shift from selecting a simple signal from a limited set of possible signals to the infinite linguistic space introduces a richness that cannot be analyzed using traditional Game Theory tools. (Illustration from )

In summary, ML can attack (a) through obtaining adequacy and predictability, widely extending experimental economics to deal with language-based non-cooperative games. However, this is still limited, as we do not handle (b), beacause obtaining training data for particular game configurations is highly costly. The missing ingredient is scalability: how can we test for behavior with a huge number of parametrizations?The set of parameters defining the game. Possible parameters in a persuasion game may include the probability that the hotel is of high quality, the payoff matrix for the players, the number of rounds played, whether the game is conducted under complete information, and the types of messages exchanged between players (choosing the signal from options or writing new piece of text) Passing the ML challenge of predictability for a small number of parametrizations does not suffice when comparing different parametrizations in order to choose a favorite one (e.g., a trading mechanism for optimizing social welfare). This is the place where the LLM revolution comes into play!

Recent research has explored how closely LLMs can approximate human behavior. Prior studies have highlighted the capacity of LLMs to perform on creativity assessments , tackle challenging stumpers , and generate human-like samples reflective of specific sub-groups in social science contexts . Additionally, some investigations have centered on determining the conditions under which LLMs could serve as substitutes for human subjects in psychological studies . In a related area, assessed LLMs by replicating well-known behavioral economics experiments.

These growing lines of research inspire to ask whether the ability of LLMs to behave like humans implies they can function as training data generators for human choice prediction . It turns out this can be done effectively for a variety of language-based games, as indicated above. As a result, we can address scalability in order to address (b) as well. We can use LLM-based simulations for a wide variety of configurations, isolating the most promising ones, and testing only these ones under actual human users.

A Rigorous Approach to LLM-Based Experimental Economics

How can we approach the above in a rigorous manner? Basically, we need to follow five steps:

1. Create a parametrization of a domain of non-cooperative economic games and formalize means to measure economic outcomes in such games.
2. Generate data sets of the variety of LLM-based interactions in the corresponding games under the variety of the parametrization.
3. For some parameterizations, perform the more classical behavioral economics lab study, where, e.g., some of (or even all) the participants are humans.
4. Compare the ability to predict human behavior using LLM data with the ability to predict human behavior based on human data.
5. Check and compare the economic outcomes for the variety of parameterizations of the LLM players, potentially selecting favorable ones and validating them with additional experiments with human subjects.

An illustration of the above is provided in . In this case, the domain is language-based non-cooperative games, as mentioned above, and includes a wide variation of parametrizations of the classical persuasion, negotiation, and bargaining settings, while the economic measures are economic efficiency, fairness, and self-gain. The main asset is a dataset and simulation software allowing further experimentation. If the community accepts this call for arms, we can basically move experimental economics to a new era. The above work is the second in a line of research making a whole parametrization for LLM-based simulation in the context of behavioral economics. The first one is reported in , and is concerned with rationality assessment, where the expected payoff is taken as a measure of comparison. The system is also flexible to allow a huge coverage and variety.

The intersection of economics and LLMs holds significant potential for advancing both fields. While current LLM Agents are designed to perform tasks aligned with operator objectives (see ), they do not yet embody the economic concept of agents operating in non-cooperative, multi-player environments. As LLMs continue to evolve, we anticipate their roles expanding to include decision-making in complex economic contexts, considering long-term gains and strategic interactions with multiple agents.

In conclusion, the integration of economics and LLMs offers an opportunity to significantly advance both fields. Thanks to the scalability and advanced capabilities of LLMs, we can overcome long-standing limitations in experimental economics, leading to unprecedented progress in economic research—both in predicting human behavior and designing optimal economic mechanisms. Integrating LLMs into economic research will also pave the way for developing sophisticated AI agents capable of operating in non-cooperative, multi-agent environments, which constitute the majority of human interactions in the world we live in.